統計學（8）

這篇文章介紹抽樣分佈。

複習：由群體觀測值計算而得之表徵值成為參數（parameter）（比如和）。由樣本觀測值計算而得之表徵稱為統計量（statistic）（比如和）。

定義：當從給定群體中反覆抽取（有放回抽取）大小為n的隨機樣本時，統計量的概率分佈稱為統計量的抽樣分佈。

以之抽樣分佈為例，利用蒙地卡羅模擬法近似抽樣分佈

齊一分佈

齊一分佈的隨機變數群體做隨機抽樣，其的抽樣分佈近似於常態分佈。且：

1. 上述常態分佈的平均數約等於其群體的平均數。
2. 當每次抽樣數量n越大，變異越小。且形狀越接近常態分佈。

指數分佈

指數分佈的隨機變數群體做隨機抽樣，其的抽樣分佈有兩種情況：

1. 當每次抽樣數量n比較小，抽樣分佈近似於右偏態分佈。
2. 當每次抽樣數量n比較大，抽樣分佈近似於常態分佈。

常態分佈

常態分佈的隨機變數群體做隨機抽樣，其的抽樣分佈近似於常態分佈。與齊一分佈幾乎相同。

的抽樣分佈

當群體變異數已知

無論群體分佈是不是常態分佈，當時，的分佈都呈現近似常態分佈。其平均數和變異數是：

中央極限定理（❗️❗️❗️）

就是我們上面剛剛講到的，無論群體分佈是不是常態分佈，當時，的分佈都呈現近似常態分佈。平均數為，變異數。

即：

如果對此做標準化，則有：

服從Z分佈。

注意，如果群體確定呈現常態分佈，則永遠呈現常態分佈，不論的大小。

當群體變異數未知

如果是從具有均值和變異數的常態群體中提取的大小為的隨機樣本的平均值，則樣本統計量：

則t值服從著名的司徒頓t分佈（Student-t distribution）。

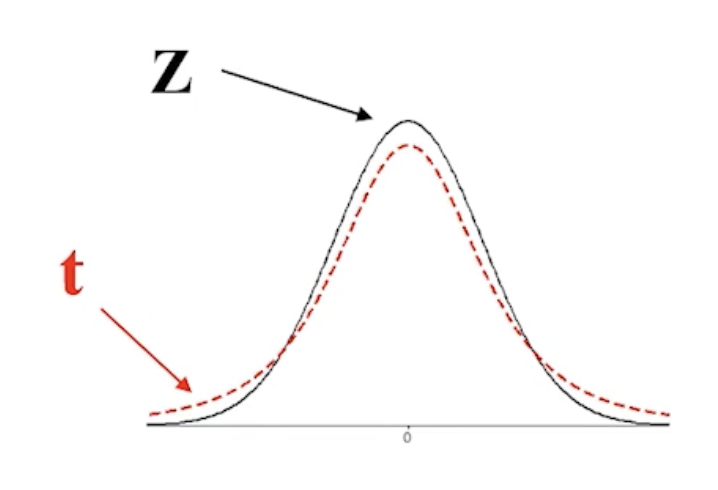
當樣本數越大，和越接近。（當，基本等同於）

自由度：，自由度控制t分佈的形狀。

由自由度可知，t分佈實際上是變動的，變動的原因是因為，分母上是，是一個近似。

司徒頓t分佈

，可以透過這個公式，在t值表中直接查到t值。

的抽樣分佈

當n足夠大，

例： A production line of light bulbs at a manufacturing company produces 5% defective items. If a random sample of 100 light bulbs is taken, what is the probability that the sample defective rate is less than 4%?

根據題目，，則。求，答案是0.3228。

群體為常態分布之其他抽樣分佈—分佈及F分佈

分佈

在一常態分佈的群體中隨機抽樣n次，且已知，則樣本之分佈統計量：

服從一個右偏分佈。自由度，自由度越大，右偏越小。

分佈和t分佈的關係：設Z爲標準常態變數，爲自由度爲的卡方變數，則有：

F分佈

兩樣本之比例（）的抽樣分佈。假設兩個常態分佈的群體，，從各自取獨立樣本。有統計量：

F機率分佈函數是一個右偏函數。