統計學（6）

這篇文章介紹連續性隨機變數及其機率分佈。

累加函數

隨機變數X之累加函數為：

不管是連續還是離散變數都適用。

離散型隨機變數尚有另一形式：

連續型隨機變數也有另一形式：，其中為連續型隨機變數的機率密度函數。

例2：一個袋子中裝有4張紙條，4張紙條上分別標註1,2,3及4，現由此袋中隨機
抽取一張紙條，令X為抽出紙條上的數字。

1. 試求X之機率函數（probability density function）。
2. 試求X之累加函數（distribution function）。
3. 試繪製X之累加函數圖。

第一問，變數X是一個離散型的隨機變數。其可能的x值為1，2，3和4，每一個數字抽取到的機率都為1/4，故其機率函數為：

第二問，離散型隨機變數的累加函數為：，注意累加函數可以寫作分段函數的形式，故本題答案是：

第三問，按照繪圖方法，繪製如下：

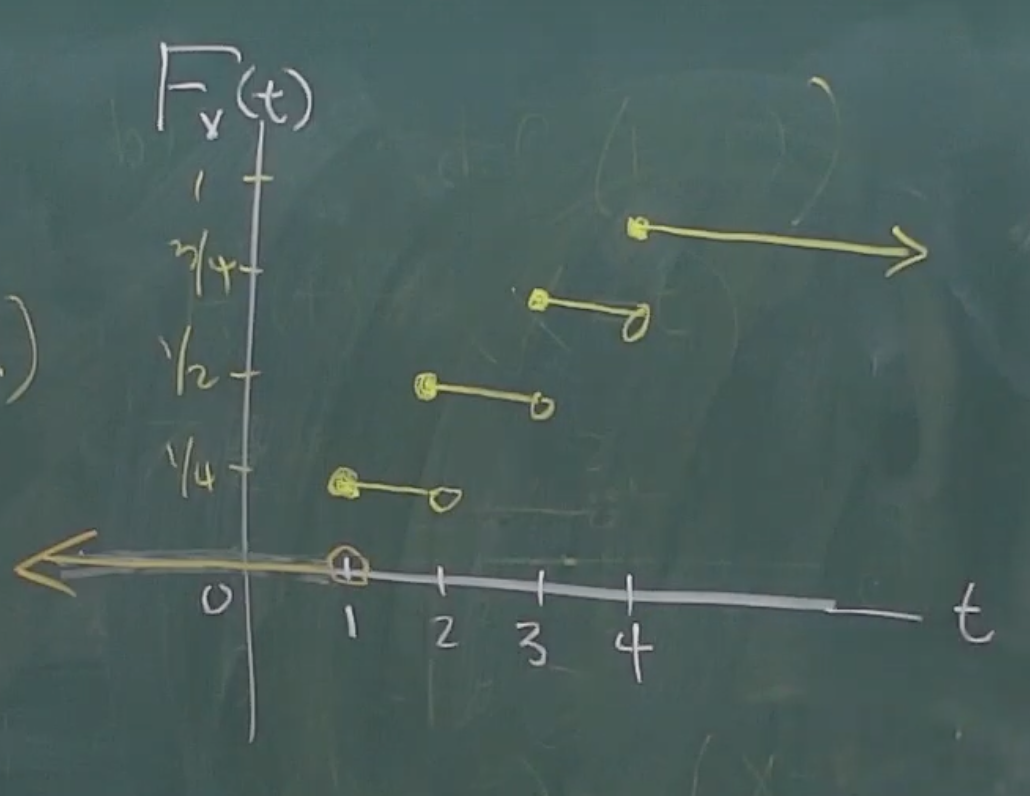
累加函數的特性

1. 若，則
4. 為一個右連續函數

一些推論：

注意，若X為離散型隨機變數，則

透過累加函數計算機率函數

對於離散型隨機變數，每一個離散值的機率，即使用每段的累加函數值減去上一段的累加函數值即可。

連續型隨機變數之機率密度函數

• 連續型隨機變數：如果一個隨機變數的累加函數是該變數的一個連續函數，則該變數為連續型隨機變數。

機率密度函數

特性：

累加函數

期望值與其他摘要量數

X為連續型隨機變數，是X的任意函數，則有的期望值：

定理：

變異數：

定理：如果變數Y滿足Y = aX + b，則有：