統計學（2）

這篇文章講統計學中的一些常用指標。

以數值指標來描述資料

• 連續型變數的四個特性：
  1. 集中趨勢（Central Tendency）
  2. 分散或變異趨勢（Dispersion or Variability）
  3. 偏態（Skewness）
  4. 峰度（Kurtosis）

集中趨勢

• 資料有往中央位置靠近的趨勢。
• 指標：
  • 平均數（mean）
  • 中位數（median）
  • 眾數（mode）

    平均數

• 群體平均數：，N為群體大小
• 樣本平均數：，n為樣本大小

中位數

• 群體中位數：
• 樣本中位數：

眾數

• 在一組資料中，出現次數最多的數值

指標使用指南

• 平均數對離群值非常敏感，而中位數和眾數不敏感。因此當資料中有離群值的時候，使用中位數或眾數，否則，使用平均數。

分散或變異趨勢

• 一組資料差異大小或數值變化的一個量數。
• 指標：
  • 全距（Range）
  • 變異數（Variance）
  • 標準差（Standard Deviation）
  • 變異係數（CV）

全距

• R = Max - Min
• 缺點：當一組數據中有離群值出現或資料筆數太多（n > 10）時，全距並非一個很好的衡量資料分散程度的量數。

變異數和標準差

• 群體變異數：
• 樣本變異數：
• 群體標準差：
  • 估計值：
• 樣本標準差：
  • 估計值：

變異係數

• 標準差和變異數是衡量一組數據絕對變異（absolute vatiation）的指標，即此指標之大小與數據的單位尺度有關係，因此，若要比較數組單位尺度不同的數據時，需使用一個衡量相對變異的指標，即變異係數。
• 群體相對變異：
• 樣本相對變異：

偏態

說明一組數據分佈的形狀。
單峰分佈的三種型態：

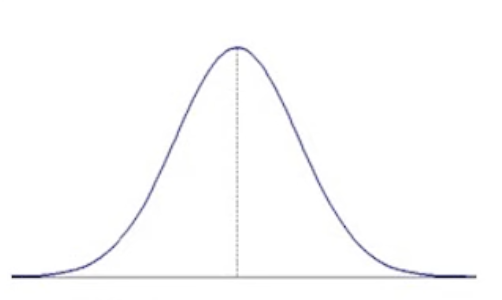
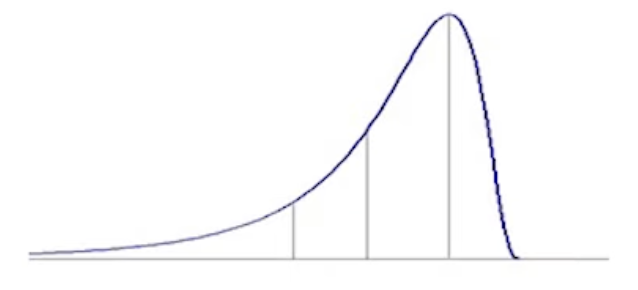
• 對稱：平均數 = 中位數
  
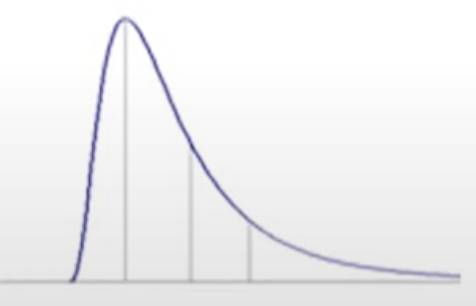
• 左偏：平均數 << 中位數
  
• 右偏：平均數 >> 中位數
  

偏態係數

樣本偏態係數：

• ：對稱
• ：右偏
• ：左偏

峰度

峰度係數

樣本峰度係數：

• ：常態峰
• ：高狹峰
• ：低闊峰

非中趨勢指標

• 百分位數
• 四分位數（, 25% - 75%）
• 中四分位距：
  • 避免極端值或離群值的干擾

數據之應用

經驗法則

如果資料呈常態分佈，則有：

• 68.26%的數據在範圍內
• 95.44%的數據在範圍內
• 99.73%的數據在範圍內

離群值：當值沒有落在範圍內，即為離群值。

柴比雪夫定理

不論連續型數據呈現什麼樣的分布狀態，至少有的數據會落在範圍內。

• 至少有0% 的數據在範圍內。（令K=1）
• 至少有55.56%的數據在範圍內。（令K=1.5）
• 至少有75%的數據在範圍內。（令K=2）
• 至少有88.88%的數據在範圍內。（令K=3）
• 至少有93.75%的數據在範圍內。（令K=4）
• 至少有96%的數據在範圍內。（令K=5）

盒鬚圖

同時展示出集中趨勢、離中趨勢、偏態、最小值、最大值等。

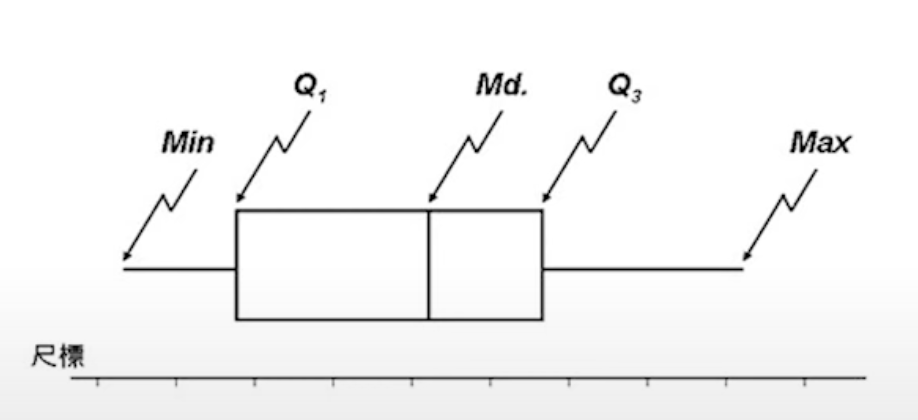
• 超過盒鬚圖之盒至距離內之值可當作離群值
• 超過盒鬚圖之盒距離外之值可當作非常可能之離群值

Z分數

Z-score是一個標準化數值，代表原始數據（）偏離其平均數（）Z個標準差。

• ：原始數據 > 平均數

• ：原始數據 < 平均數
• ：原始數據 = 平均數

加權平均

• 群體加權平均：
• 樣本加權平均：